Want a semi-simple explanation of magnetic resonance? Click to jump directly to it.
This page supplements the article Is Quantum Mechanics necessary for understanding Magnetic Resonance? by Lars G. Hanson appearing in Concepts of Magnetic Resonance A. It is not a critique of Quantum Mechanics (QM) that provides useful descriptions of spin physics including NMR/MRI, but the article warns against some common QM-inspired mistakes. In the article, Quantum mechanics is employed to prove frequent errorneous statements wrong. These issues were also discussed in talks, e.g. at the MMCE.
This web supplement provides alternatives to QM-inspired explanations that often raise more questions than they answer. This problem is especially severe in the MRI literature where a classical description is fully adequate. Like other basic phenomena, MR can be explained using Quantum Mechanics, but all aspects of basic MR can alternatively be explained using intuitive classical mechanics. The complexity of Quantum Mechanics (QM) have led authors to introduce numerous errors in MR tutorials, but when corrected, QM descriptions are very close to the classical description. There are good reasons to go beyond classical descriptions when describing NMR spectroscopy of coupled nuclei, but classical intuitive insight is an important starting point.
A book chapter supplementing the mentioned article is entitled The ups and downs of NMR described by classical and quantum mechanics (preview below). It focuses on the connection between classical and quantum descriptions of NMR, including the validity of spin visualization from a quantum perspective. Unlike some typical figures used in MR introductions, the figures below are valid, if interpreted with care. Reviews of the book edited by Csaba Szántay Jr. are available at Amazon.
The text below is targeted at people in need of explaining magnetic resonance, and the level of detail is inadequate for new students. A longer tutorial provides additional explanations of MRI basics and techniques (48 pages). Links are also given to free software that facilitates MR-teaching and may improve understanding considerably. It is not necessarily recommended to use the figures below for teaching (depends on the focus), but it is certainly recommended to avoid some misleading figures that often appear in MRI text books, as discussed in the article mentioned above that has triggered a number of reader comments.
Magnetic Resonance explained
The atomic nucleus of hydrogen (a proton) behaves like a small magnet with a north and a south pole (a magnetic dipole). Like compass needles, protons tend to align along the direction of an applied magnetic field. Hence, a sample that contains hydrogen atoms will be magnetized by the field. The sample literally acquires a north and a south pole.
If a compass needle in rest is given a push, it will oscillate about the north direction before it eventually comes to rest. As long as the needle oscillates, it will generate an oscillating magnetic field (emit radio waves). If, for example, the needle swings three times per second, the generated field will have a 3 Hz frequency. The reverse process occurs if the compass is subject to an oscillating field from an external source that push an initially resting needle in synchrony with its natural oscillation frequency: The needle will start swinging and the oscillation will gain amplitude, just as a child in a swing will, if it is pushed in synchrony with its natural motion.
These aspects can be explored with the CompassMR simulator that will leave students with a good understanding of the basic MR phenomenon after a few minutes.
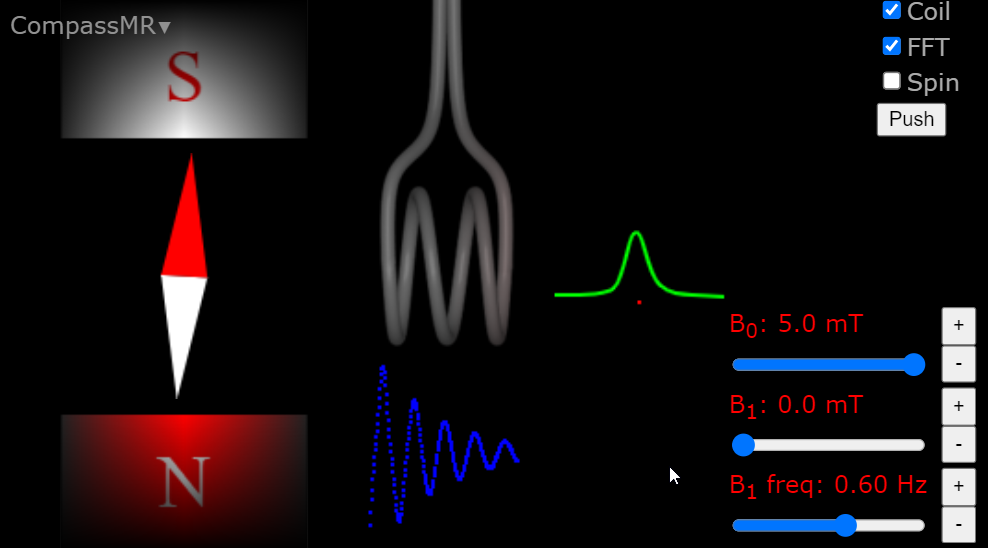 |
| Explore the resonance phenomenon for compass needles and nuclei directly in you browser (click figure). Try to make the needle oscillate significantly in a strong magnetic field by pushing it with a weak, resonant magnetic field. When the needle oscillates, the generated field oscillations can be detected with a coil. Alternatively, see YouTube demonstration. |
Similarly, the magnetization of a magnetized sample can be pushed away from equilibrium by an oscillating field - even if weak - if it is applied at the resonance frequency. Afterwards when the external oscillating field is turned off, field oscillations caused by the sample will persist, as long as the oscillation is ongoing. This is the MR signal that increases with the amplitude of the oscillation.
A traditional compass in a magnetic field will eventually come to rest and will point toward north. The situation is different for nuclei in a liquid, as these are bouncing off each other due to random nuclear motion (diffusion). The nuclei experience random interactions with their ever-changing local environment. Hence the nuclear "compass needles" continuously experience tiny magnetic pushes that change randomly. At room temperature, the energies associated with thermal collisions are much higher than needed to reorient a nucleus in a magnetic field. The nuclei are well shielded, however, and only interact weakly with environment. Hence they are only significantly disturbed on time scales of, e.g., 100 ms. During such a period, the nuclei in a liquid have "collided" (interacted magnetically) with vast amounts of other nuclei, but since the resulting pushes are weak and random, the spin motion (precession) is virtually indistinguishable from that of non-interacting particles over relatively long periods (a millisecond is long when compared to the time scale of precession, and to the correlation time defined as the typical time between changes in the local environment of a nucleus).
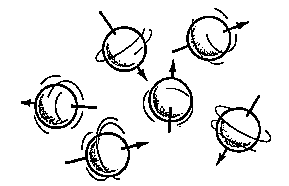
The situation can be compared to that of compasses bouncing in a running tumble drier: The compasses will never be left alone long enough for the needles to come to rest pointing toward north. Nevertheless, there will be a tendency for the compasses to point north. The individual needle does not reach a steady state, while the distribution of needle directions rapidly will. This equilibrium distribution is nearly spherical but slightly skewed toward north. Hence, the net magnetization of many bouncing compasses or nuclei is essentially at rest and points toward north as shown here:


Equilibrium magnetization before and after application of a strong magnetic field that polarizes the sample as reflected in increased density of arrows in the direction of the field. The magnetic field also makes the spin distribution rotate around the direction of the field (here vertical). Click figures to enlarge. The book chapter preview below describes in detail why these figures are better representations of thermal equilibrium than some typical figures, also from a QM perspective.
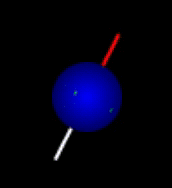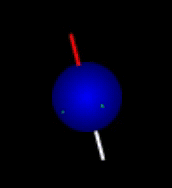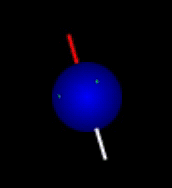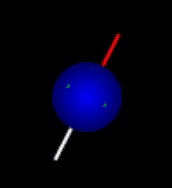 |
|
Spin makes protons magnetic along the spin axis as shown in the first figure above. The spin axis itself precesses (rotates) around the direction of the applied magnetic field which is pointing upwards in the current figure illustrating both spin and precession classically (from the CompassMR simulator). |
There are differences between compass needles and protons worth mentioning at this point. Whereas compass needles will swing through north, the motion of the proton magnetic moment is precession around the north direction (vibration vs. precession). The difference originates from a peculiar nuclear property: All protons appear to be spinning at a particular rate, whether or not they are in a magnetic field. In fact, the magnetic property of nuclei is a consequence of this spin that makes each of them magnetic along its spin axis. Hence protons behave like normal bar magnets that happen to be spinning around their north-south axis (note: the spin axis is in general different from the precession axis). A hypothetical compass needle spinning like this would, if unrestrained, also precess around north rather than swing directly toward this direction (due to its angular momentum). Similarly, a spinning top will slowly precess around the direction of the gravitational field. This difference between nuclei and normal compass needles is not of fundamental importance for the MR phenomenon, but it is certainly worth keeping in mind. The emitted oscillating field is, for example, rotating due to the precession. Similarly, the field used for exciting the nuclei is preferably also rotating. There is another related difference between proton precession and normal compass needle oscillation: The proton precession frequency depends only on the field whereas the vibration frequency of a compass needle also depends on the amplitude of oscillation, except when the oscillations are small.
| Non-interacting protons precess like classical spinning, charged spheres in an external field. The Larmor frequency is common for the nuclei, but their phase and degree of excitation differ. The spin and precession axis coincide for the top-left sphere (from the CompassMR simulator). |
Generally, a magnetic field makes the near-spherical spin distribution rotate around the direction of the field. Hence, a static field makes it rotate around a fixed axis. An additional resonant, circularly polarized RF field is characterized by a field vector that is orthogonal to the static field, and stationary relative to the rotating spin distribution. The spins will precess around this rotating field vector. This motion is complicated as seen in the animation below, but simple when described in a rotating frame of resonance. The animation shows how a resonant RF pulse can rotate the spin-distribution away from equilibrium - and back:
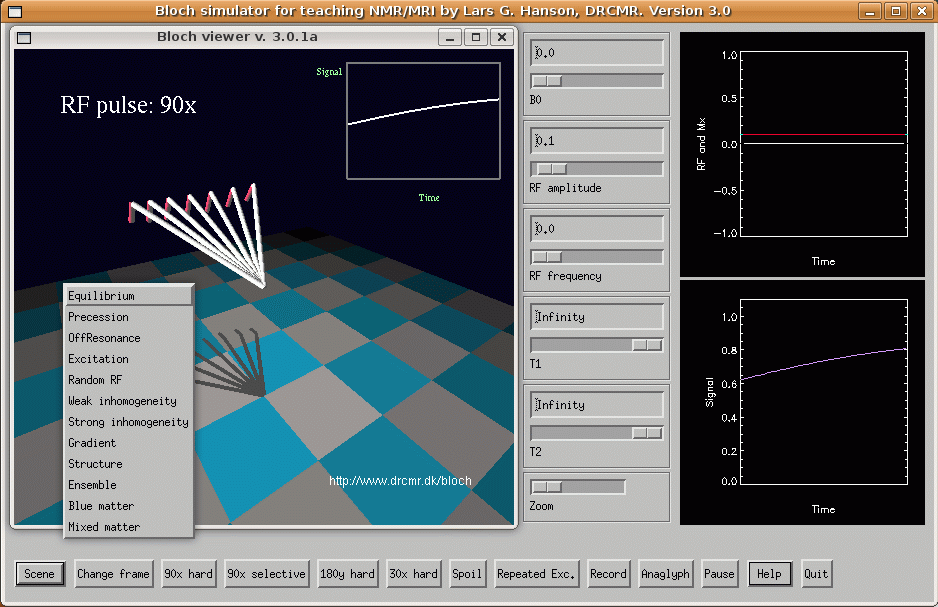
Animation showing the orientation distribution of the magnetic dipoles (spins) before and during excitation. The main magnetic field makes the ensemble of nuclei precess, and skews the spin distribution toward the direction of the field as indicated by the density of spins initially being higher along this direction (vertical in the figure). When a resonant radio frequency (RF) field is applied, the entire magnetization distribution is rotated around an axis that is rotating perpendicularly to the magnetic field. The resulting motion of the net magnetization is illustrated with the circular arrow. A resonant field can make the magnetization perform a full 360-degree rotation as shown in the animation, but normally smaller tip angles are used, e.g. 90 or 180 degrees. Further aspects of spin dynamics can be explored interactively using the Bloch simulator. Click figure to enlarge or here for even larger version.
The effect of a resonant field is also illustrated below, but in a frame of reference rotating at the resonance frequency, which simplifies the motion much. The figure shows the rotation of the magnetization distribution resulting from application of a resonant RF pulse.


A resonant RF field rotates the equilibrium magnetization in the rotating frame of resonance. Click figures to enlarge.
In addition to the externally applied fields, each nucleus experiences fluctuating magnetic fields generated by other nuclei that it happens to meet. Only if these random RF fields approximately fulfill the resonance condition, i.e., occasionally push the magnetization in synchrony with the precession, will they be effective in changing the spin energy that is proportional to the longitudinal magnetization. Such inelastic interactions are needed for T1-relaxation to occur and T1 is consequently minimal when the correlation time equals the precession period. Whereas energy-preserving elastic interactions do not change the longitudinal magnetization, they can still change the transversal phase relations and therefore cause irreversible coherence loss, i.e., T2-relaxation. In other words: Each of two neighboring nuclei will precess in the static field and in the field generated by the other (spin-spin interaction), but this process cannot change the total longitudinal magnetization since energy is preserved. Only when the environment (lattice) acts as a reservoir or supply of energy, can magnetic interactions change the longitudinal magnetization. Therefore T2- and T1-relaxation are sometimes called spin-spin and spin-lattice relaxation, respectively. Since all interactions cause T2-relaxation but only a subset cause T1-relaxation, T2 is always shorter than T1.
Further details are provided in the mentioned publications and in lecture notes. Outlines of proofs based on quantum mechanics are in the article Is Quantum Mechanics necessary for understanding Magnetic Resonance? It should be stressed that quantum mechanics is not superfluous for physics and chemistry students, for example, who will engage in spectroscopy or in detailed calculations of relaxation. However, It is believed that all MR students will benefit from learning a correct, intuitive and precise classical description. The connection between classical and quantum NMR descriptions is described in depth in a the book chapter The ups and downs of NMR described by classical and quantum mechanics (introduced above, preview below).
The award-winning "Bloch Simulator" that provides additional insight into many MR techniques. See https://www.drcmr.dk/bloch
Book chapter preview addressing the relation between classical and quantum descriptions of magnetic resonance (page 141 to 171. Scrolling back and forth may help).
Excerpt from "Anthropic Awareness - The Human Aspects of Scientific Thinking in NMR...", 32 pages, edited by C Szántay, Jr., Elsevier, 2015.
Access via ScienceDirect and Google Books. Reviews are available at Amazon.
Slides addressing the connection between classical and quantum MR descriptions.