Data Download and Analysis
Step-by-step Guide
- Download the dataset in NifTI format by registrating here. The Zip-file contains the matlab files for analyzing the data
- Extract the Zip-file to (folder: DPFG5_dataset)
- Download the tools for NIfTI and ANALYZE images from the Matlab Central file exchange and add it to the path in DPFG5_analysis.m
- Run the DPFG5_analysis.m scripts in the DPFG5_dataset folder
DPFG-5 design gradient directions
A MATLAB function for generating the gradient direction scheme of the DPFG-5 design can be downloaded here
Overview
Purpose: Pulsed field gradient diffusion sequences (PFG) with multiple diffusion encoding blocks offer new microstructural tissue information, such as contrast for nonspherical compartment shapes in macro- scopically isotropic samples, i.e. samples with negligible directional signal dependence on diffusion gradients in standard diffusion experiments. However, current acquisition schemes are not rotationally invariant in the sense that the derived metrics depend on the orientation of the sample, and are affected by the interplay of sampling directions and compartment orientation dispersion when applied to macroscopically anisotropic systems. Here we propose a new framework, the d-PFG 5-design, to enable rotationally invariant estimation of double wave vector diffusion metrics (d-PFG). Using the d-PFG 5-design we measure the apparent compartment eccentricity as a source of new microstructural MRI contrast and is potentially usefull in resolving complex fiber configurations.
Method: The method is based on the idea that an appropriate orientational average of the signal emulates the signal from a powder preparation of the same sample, where macroscopic anisotropy is absent by construction. Our approach exploits the theory of exact numerical integration (quadrature) of polynomials on the rotation group, and we exemplify the general procedure with a set consisting of 60 pairs of diffusion wave vectors (the d-PFG 5-design) facilitating a theoretically exact determination of the fourth order Taylor or cumulant expansion of the orientationally averaged signal.
Results: The d-PFG 5-design is evaluated with numerical simulations and ex vivo high field diffusion MRI experiments in a nonhuman primate brain. Specifically, we demonstrate rotational invariance when estimating compartment eccentricity, which we show offers new microstructural information, complementary to that of fractional anisotropy (FA) from diffusion tensor imaging (DTI). The imaging observations are supported by a new theoretical result, directly relating compartment eccentricity to FA of individual pores.
Below you will find a description of the imaging dataset used in Jespersen et. al. 2013, which is also available for download along with MATLAB scripts for processing the data. MATLAB scripts for reproduction of the simulation results are available for download. Lastly a the DPFG-5 design gradient directions used for data acquisistion are avaialble for download. Please see Jespersen et. al. 2013 for further details.
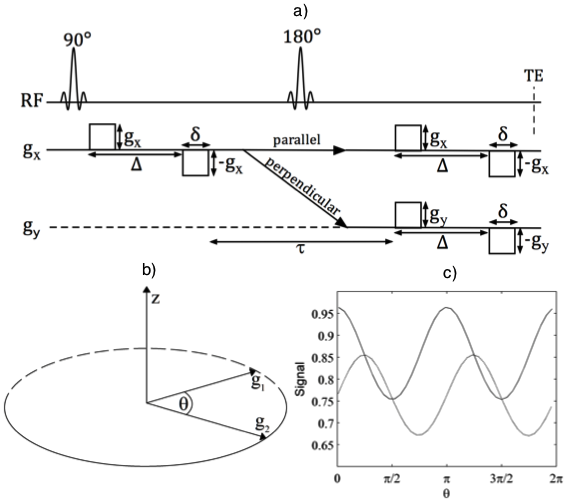 |
| Figure 1 (Jespersen et. al. 2013). The d-PFG experiment used in this study was realized in a single spin-echo sequence with two individual bipolar diffusion encodings on each side of the refocusing pulse (a). The two bipolar gradient pairs on each side of the 180° pulse have identical timing parameters Δ and δ as well as strength g. g1 and g2 are applied in either parallel or orthogonal directions according to the d-PFG 5-design (see Jespersen et. al. 2013 figure 2 for further details), but here they are shown only along x and y directions for concreteness. The sampling of the diffusion gradients in angular d-PFG is shown in (b). The corresponding angular modulation of the signal depends on the absolute directions of the gradients in anisotropic systems (c), but not in isotropic systems. The curves in (c) were produced using simulations of particles in an anisotropic medium consisting of spheroids (short semi-axis 1 μm, long semi-axis 4 μm) oriented according to a Watson distribution with concentration parameter 10 and main direction along the z-axis. The wave vectors are varied in the yz-plane, and for the solid line the parallel direction is along the x-axis, whereas for the dashed line the parallel direction is 45 degrees from the z-axis. © 2013 John Wiley & Sons, Ltd |
Imaging Dataset
A perfusion fixated brain from a normal 32month Vervet monkey was used for the experiment. The brain was prepared using an optimized procedure for post mortem diffusion MRI (Dyrby et al. 2011). To facilitate the use of a high signal/small field of view surface coil, a whole sagittal section was dissected covering ~5mm from the midsagittal plane over the left hemisphere. The live monkey was handled and cared for on the Island of St. Kitts according to a protocol approved by the local ethics committee (The Caribbean Primate Center of St. Kitts). Imaging was performed on a Varian 4.7 T animal scanner with a 12 cm bore using a volume coil for transmission and a 20 mm diameter surface coil for signal reception. A d-PFG sequence was realized in a single spin-echo layout with one bipolar diffusion encoding on each side of the 180° pulse (the basic sequence layout is shown in Figure 1(a)); single-line readout was used. Images were acquired with a 128 × 64 matrix at 0.6 mm3 isotropic resolution with 12 slices and TR/TE = 2500/54 ms, using a spin-echo single line readout with four averages. The imaging time for one image volume was 4 min and each experiment took 10 hours 40 min. The gradient strength, separation and duration of the two encodings were identical and set to G = 0.49 T/m, Δ = 11 ms and δ=3ms, giving q=0.56/μm and a net b value of b=3.1ms/μm², and the directions of the individual gradient pairs were set according to our d-PFG 5-design scheme. The mixing time separating the two gradient pairs was 15 ms. The mixing time and the effective diffusion time of the individual diffusion encodings were set low to reduce relaxation effects but large enough to neglect time dependence on DTI metrics. Stable metrics are observed in the range above 10ms and time dependence is observed only for diffusion times below 5 ms. The protocol was repeated once with a randomly rotated set of gradient directions to assess rotational invariance, and once using G = 0.346 T/m (with the original gradient directions) to investigate the effect of gradient strength. In the latter case, q=0.27/μm and the resulting b value was 1.5 ms/μm². Instead of acquiring an additional standard DTI data set, fractional anisotropy (FA) was determined using the d-PFG data corresponding to the parallel wave vectors of the low gradient acquisition.
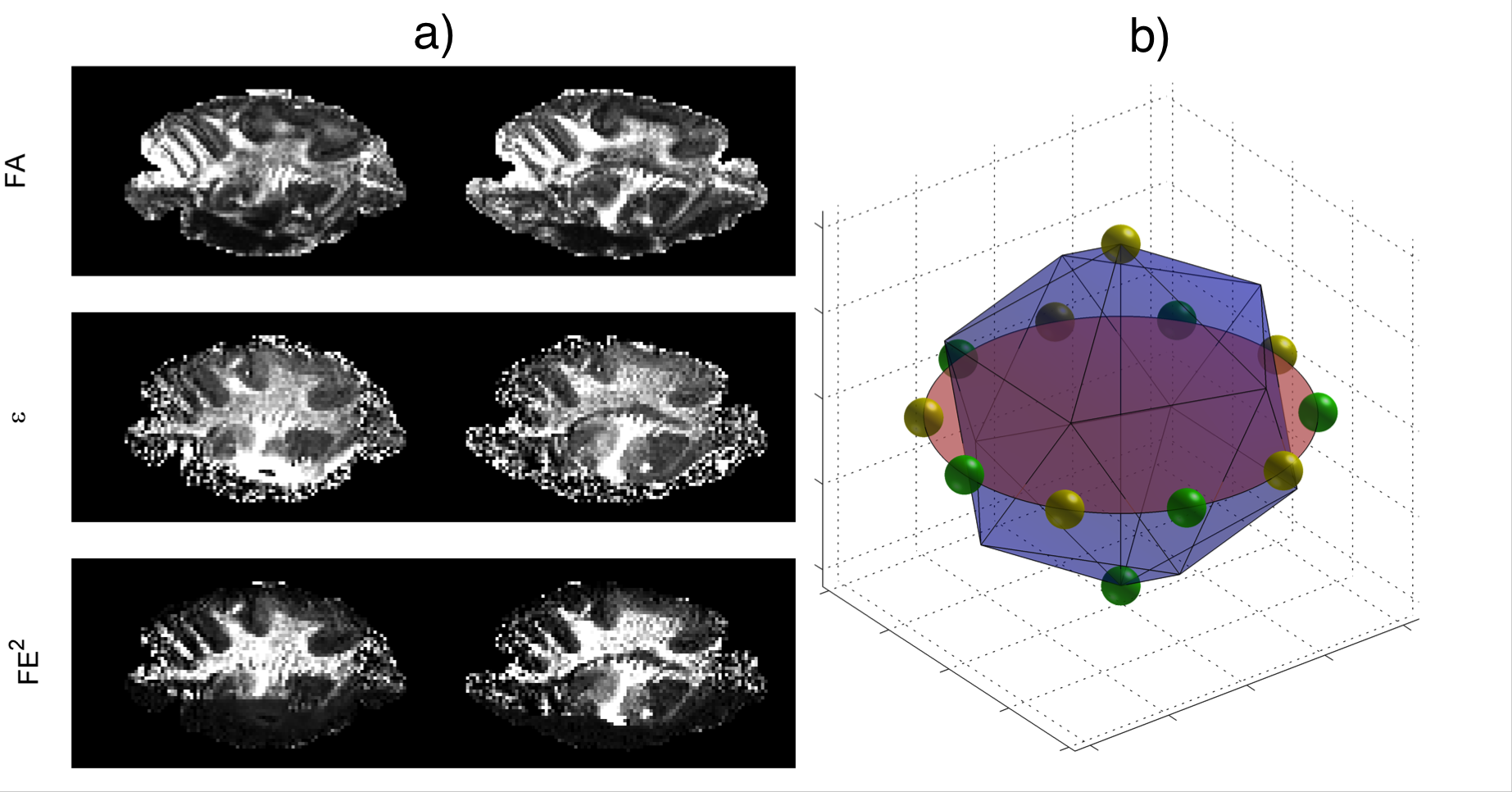 |
|
a) Fractional compartment eccentricity (FE²) is shown alongside FA and apparent compartment eccentricity(ε), and b) the directions of the second wave vector are related to the first wave vector as 10 points evenly distributed on the associated great circle. © 2013 John Wiley & Sons, Ltd |
Simulations
Simulations for diffusion in spheroids with reflecting boundary conditions were implemented in Matlab using Monte Carlo methods with 100 000 particles, a diffusion constant of 2 μm2/ms, and time step 1μs. While the bulk ‘free’diffusivity for intracellular water is not precisely known, we chose a value to reflect the diffusivity of water at room temperature, corresponding to the imaging experi- ments; see later. If necessary, the simulation results can be translated to other values of the diffusivity by scaling the diffusion times accordingly. The spheroids, i.e. cylindrically symmetric ellipsoids, had short semi-axes of a=b=1μm and long semi-axes c of 2, 4 and 8 μm, all appropriate microstructural dimensions for biological tissue. 50 directions were generated from a Watson distribution with concentration parameters κ between 0 and 20, and were used as the directions of the long axes of the 50 spheroids. The Watson distribution, which has previously been used to model neurite dispersion, is a cylindrically symmetric bimodal distribution of directions, and as the concentration parameter κ grows from 0, the distribution of directions changes from isotropic (κ = 0) to being increasingly concentrated around the main direction z. Values for the diffusion wave vectors were chosen between 0 and 1.5μm with directions from the d-PFG 5-design, and the diffusion times were linearly spaced between zero and 30 ms (c = 2 μm), 120 ms (c = 4 μm) and 480 ms (c = 8 μm). The diffusion gradient shapes were assumed to be square pulses with a duration of one time step. Aiming to reach the large mixing time regime, mixing times were kept fixed at the largest diffusion time in each case. We evaluated apparent compartment eccentricity using Equation [9] (see Jespersen et. al. 2013) against the true value ε = 2(a²-c²)²/375 for spheroids. For comparison, we furthermore obtained estimates of IMA using the 15 directions suggested in (Lawrenz et. al. 2010), all other parameters being the same.
Please cite the following papers:
1) Describing the new theory, method and how the data was acquired:
Jespersen, S. N., Lundell, H., Sønderby, C. K. and Dyrby, T. B. (2013), Orientationally invariant metrics of apparent compartment eccentricity from double pulsed field gradient diffusion experiments. NMR Biomed.doi: 10.1002/nbm.2999
2) Describing the preparation of the vervet monkey brain tissue:
Dyrby TB, Baaré WFC, Alexander DC, Jelsing J, Garde E, Søgaard LV. An ex vivo imaging pipeline for producing high-quality and high resolution diffusion-weighted imaging datasets. Hum Brain Mapp 2011;32:544–563
Funding
S. J. was supported by the Danish Ministry of Science, Technology and Innovation's University Investment Grant (MINDLab). H. L. and C. K. S. was partially supported by the project ‘CONNECT’, which acknowledges thefinancial support of the Future and Emerging Technologies (FET) program within the Seventh Framework Program for Research of the European Commission, under FET-Open grant No 238292. T. D. was partially funded by a grant of excellence by the Lundbeck Fonden on the Control of Action (grant No R59 A5399).
References
Lawrenz M, Koch MA, Finsterbusch J. A tensor model and measures of microscopic anisotropy for double-wave-vector diffusion- weighting experiments with long mixing times. J. Magn. Reson. 2010; 202(1): 43–56.



